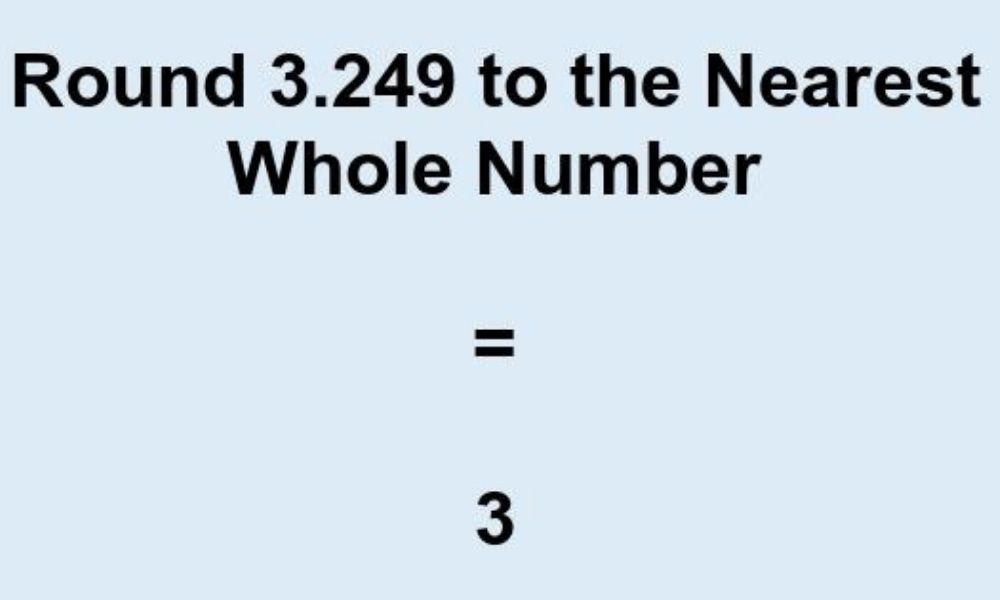When dealing with numbers, it is often necessary to round them to a specific decimal place. Rounding helps simplify calculations and provides a more manageable representation of a value. In this article, we will explore the process of rounding and specifically focus on rounding the number 3.249 to the nearest tenth.
Contents
Understanding Rounding
Rounding is a mathematical process that involves approximating a number to a specified decimal place. It is commonly used to simplify calculations, improve readability, and provide a more practical representation of a value. When rounding a number, we determine which value it is closest to based on the specified decimal place.
For example, if we want to round a number to the nearest whole number, we look at the decimal part of the number. If the decimal part is less than 0.5, we round down to the previous whole number. If the decimal part is 0.5 or greater, we round up to the next whole number.
Rounding to the Nearest Tenth
When rounding to the nearest tenth, we focus on the first decimal place after the decimal point. In the case of 3.249, the digit in the tenths place is 4. To determine whether we round up or down, we look at the digit in the hundredths place, which is 9 in this case.
Read:What you need to know about aviation business dvcodes?According to the rounding rule, if the digit in the hundredths place is 5 or greater, we round up. If it is less than 5, we round down. In the case of 3.249, the digit in the hundredths place is 9, which is greater than 5. Therefore, we round up the digit in the tenths place, which is 4, to the next whole number, resulting in 3.3.
Examples of Rounding to the Nearest Tenth
Let’s explore a few more examples to solidify our understanding of rounding to the nearest tenth:
- 4.712 rounds to 4.7
- 8.956 rounds to 9.0
- 2.345 rounds to 2.3
- 6.899 rounds to 6.9
In each of these examples, we look at the digit in the hundredths place to determine whether to round up or down. If the digit is 5 or greater, we round up, and if it is less than 5, we round down.
Case Studies: Rounding in Real-Life Scenarios
Rounding is not just a mathematical concept; it has practical applications in various real-life scenarios. Let’s explore a few case studies where rounding plays a crucial role:
Read:What’s next database?1. Financial Calculations
In financial calculations, rounding is often used to simplify values and provide a more practical representation of monetary amounts. For example, when calculating interest rates or loan payments, rounding to the nearest cent can make the numbers more manageable and easier to understand.
Consider a scenario where you have a loan with an interest rate of 4.875%. Rounding this value to the nearest tenth makes it 4.9%, which is easier to work with in calculations.
2. Statistical Analysis
In statistical analysis, rounding is commonly used to present data in a more concise and understandable format. When dealing with large datasets, rounding can help reduce the complexity of numbers and make them more accessible to a wider audience.
For example, if you are analyzing a dataset of population sizes in different cities, rounding the numbers to the nearest thousand can provide a clearer picture of the data. Instead of dealing with precise values like 1,234,567, rounding to 1,235,000 simplifies the presentation without significantly impacting the overall analysis.
3. Measurement and Engineering
In fields such as measurement and engineering, rounding is crucial for practical purposes. Precise measurements often involve decimal values that can be challenging to work with in real-world applications. Rounding helps simplify these values and ensures practicality in calculations and designs.
Read:What do guys think of a funny girl?For instance, when designing a bridge, engineers need to work with measurements that are practical and feasible to implement. Rounding measurements to the nearest inch or centimeter allows for easier construction and ensures that the bridge meets safety standards.
Summary:
Rounding is a mathematical process used to approximate numbers to a specified decimal place. When rounding to the nearest tenth, we focus on the digit in the hundredths place to determine whether to round up or down. Rounding has practical applications in various fields, including finance, statistics, and engineering.
Understanding how to round numbers is essential for simplifying calculations, improving readability, and providing practical representations of values. Whether you are dealing with financial calculations, statistical analysis, or engineering designs, rounding plays a crucial role in ensuring accuracy and practicality.